بررسی پارامتر های مختلف بر طیف پاسخ زلزله

عوامل مختلفی بر روی طیف های زلزله موثر می باشد و هدف ما،
بررسی نحوه ی تاثیر این عوامل بر روی طیف های زلزله می باشد.

مهمترین این موارد به شرح زیر می باشد:

1- نوع خاک منطقه

2- بزرگی زلزله (ریشتر)

3- مکانیزم نوع گسل

4- فاصله

5- مدت زمان

در این پروژه تاثیر چهار عامل اول را بر روی طیف های
پاسخ بررسی میکنیم

دریافت فایل

عنوان: بررسی پارامتر های مختلف بر طیف پاسخ زلزله
حجم: 1.16 مگابایت
توضیحات: بررسی پارامتر های مختلف بر طیف پاسخ زلزله

اختلاف زیاد بین برش پایه استاتیکی و طیفی

سوال: من تو یک پروژه ای تحلیل طیفی انجام دادم منتها بین برش پایه استاتیکی و طیفی اختلاف خیلی زیادی وجود داره، میشه گفت بیش از 100 برابره
آیا اشکالی داره یا با همین نتایج عملیات همپایه سازی انجام بدم؟

پاسخ:

اگر طیف بی بعد شده B را از مسیر Define menu > Functions > Response Spectrum تعریف نموده‌اید و سپس اقدام به تعریف حالت بار طیفی با ضریب مقیاس AI/R کرده‌اید، نبایستی پراکندگی زیادی با برش پایه استاتیکی ایجاد شود. اگر 100 برابر برش‌های پایه استاتیکی و دینامیکی با هم اختلاف دارند، به احتمال زیاد خطای عددی یا خطای مدلسازی دارید و موارد زیر را کنترل نمایید:
1- کنترل کنید که تعداد مودهای نوسانی در نظر گرفته شده حداقل 90% جرم را جذب کرده باشد. در مواردی که تغییرات زیاد سختی در ارتفاع داشته باشید (مثل حالتی که در طبقاتی دیوار حائل وجود داشته باشد) نیاز به مودهای نوسانی زیادتری از حالات معمول داریم. برای تعریف مودهای ارتعاشی باید از مسیر Define menu > Modal Cases اقدام نمایید.
2- کنترل کنید که ضریب مقیاس را درست وارد کرده باشد و حتما آن را براساس واحد برنامه وارد نمایید. مثلا ممکن است که واحد شتاب برنامه mm/sec^2 بوده و شما مقدار g (شتاب ثقل) را بر اساس واحد m/sec^2 برابر 9.81 وارد کرده باشد که در این حالات 1000 برابر ضریب مقیاس کم بدست می‌آید و یا مثلا ضریب مقیاس بر اساس cm/sec^2 بوده و شما آن را 9.81 وارد کرده‌اید که ضریب مقیاس 100 برابر کمتر حاصل می‌شود.
3- ناپایداری‌های سازه را بررسی کنید. سازه نباید در بخشی از آن دارای سختی ناچیز باشد.
4- جرم سازه را کنترل کنید.
منبع:@AlirezaeiChannel

هم پایه سازی برش پایه در تحلیل طیفی

طبق بند 3-4-1-4 استاندارد 2800، در مواردی که برش پایه طیفی کمتر از استاتیکی شود، باید بازتاب های سازه (مثل لنگرها، برش ها و ...) به نسبت برش پایه استاتیکی (که بیشتر است) به دینامیکی (که کمتر است) افزایش داده شود. اگر برش پایه دینامیکی بیشتر شد (که اغلب این مورد اتفاق نمی افتد مگر اینکه سازه را زیادی سخت مدل کرده باشید) بایستی ضریب مقیاس دینامیکی همان AI/R باشد.

نجلیل استاتیکی ، طیفی، دینامیکی و تاریخچه زمانی

۱-روش های خطی
-تحلیل استاتیکی معادل
-دینامیکی طیفی
-دینامیکی تاریخچه زمانی

..............................................
 تحلیل استاتیکی خطی：

فرضیات اساسی روش تحلیل استاتیکی خطی عبارتند از :

1 ـ رفتار مصالح خطی است .

2 ـ بارهای ناشی از زلزله ثابت ( استاتیکی ) است .

3 ـ کل نیروی وارد بر سازه برابر ضریبی از وزن ساختمان است .

در این روش نیروی جانبی ناشی از زلزله طوری انتخاب می شود که برش پایه حاصل از آن برابر نیروی برش پایه مطابق روابط آیین نامه شود. مقدار برش پایه در این روش چنان انتخاب شده است که حداکثر تغییر شکل سازه با آنچه که در زلزله سطح خطر مورد نظر پیش بینی می شود مطابقت داشته باشد. چنانچه تحت اثر بار وارده، سازه به طور خطی رفتار کند، نیروهای بدست آمده برای اعضای سازه نیز نزدیک به مقادیر پیش بینی شده هنگام زلزله خواهند بود، ولی اگر سازه رفتار غیر خطی داشته باشد، نیروهای محاسبه شده از این طریق بیش از مقادیرجاری شدن مصالح خواهند بود.  به همین جهت هنگام بررسی معیارهای پذیرش نتایج حاصل از تحلیل خطی برای سازه هایی که هنگام زلزله رفتار غیر خطی دارند، اصلاح می گردد.

 

---

 

 تحلیل دینامیکی خطی：

تحلیل دینامیکی خطی می تواند به دو روش طیفی یا تاریخچه زمانی انجام شود. فرضیات خاص این روش در محدوده رفتار خطی عبارتند از :

1 ـ رفتار سازه را می توان بصورت ترکیبی خطی از حالت های مودهای ارتعاشی مختلف سازه که مستقل از یکدیگرند محاسبه نمود .

2 ـ زمان تناوب ارتعاشات سازه در هر مود در طول زلزله ثابت است .

در این روش ، مشابه روش تحلیل استاتیکی خطی، پاسخ سازه در زلزله سطح خطر مورد نظر در ضرایبی ضرب می شود تا حداکثر تغییر شکل سازه با آنچه که در زلزله پیش بینی می شود مطابقت داشته باشد. به همین علت نیروهای داخلی در سازه های شکل پذیر که در هنگام زلزله رفتار غیر خطی خواهند داشت بزرگتر از نیروهای قابل تحمل درسازه برآورد می شوند. به همین جهت هنگام بررسی معیارهای  پذیرش در نتایج حاصل از تحلیل خطی برای سازه هایی که هنگام زلزله رفتار غیر خطی دارند، اصلاح می گردد.  

 

---

 

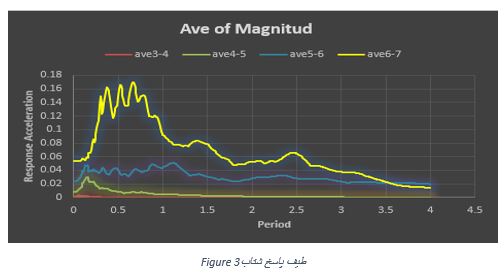
روش تحلیل طیفی：

تعداد مودهای ارتعاشی در تحلیل طیفی چنان باید انتخاب شود که جمع درصد مشارکت جرم مؤثر برای هر امتداد تحریک زلزله در مودهای انتخاب شده حداقل 90% باشد . بعلاوه در هر امتداد، حداقل باید سه مود اول نوسان و حداقل تمام مودهایی که دارای زمان تناوب بیش از 4% ثانیه هستند در نظر گرفته شوند . طیف طرح مورد استفاده در این روش باید مطابق آیین نامه انتخاب شود .

نتایج حاصل از هر مود نوسان باید با روشهای آماری شناخته شده مانند جذر مربعات  SRSSروش ترکیب مربعی کامل (CQC) و یا روش‌های دقیق‌تر که اندرکنش بین مودها را دقیقتر درنظر می گیرد، انجام شود.

اثر زلزله در امتداد عمود بر امتداد مورد نظر در صورت لزوم باید در نظر گرفته شود .

 

---

 

 روش تحلیل تاریخچه زمانی：

در تحلیل تاریخچه زمانی ، پاسخ سازه با استفاده از روابط دینامیکی در گام های زمانی کوتاه محاسبه می شود. در این روش باید پاسخ سازه تحت تحریک شتاب زمین بر اساس حداقل سه شتاب نگاشت محاسبه شود. چنانچه کمتر از هفت شتابنگاشت برای تحلیل انتخاب شود باید بیشینه اثر آنها برای کنترل تغییر شکل‌ها و نیروهای داخلی منظور شود. چنانچه از هفت شتابنگاشت یا بیشتر استفاده شود می توان مقدار متوسط اثر آن‌ها را برای کنترل تغییر شکل‌ها و نیروهای داخلی در نظر گرفت.

تفاوت روش CQC و SRSS در تحلیل دینامیکی طیفی

در آنالیز طیفی، پاسخ نهایی سازه با استفاده از ترکیب مودهای مختلف آن بدست آورده می شود.  در واقع پاسخ سازه به صورت ترکیبی از شکل‌های مودی مختلف است. برای هر مود در نظر گرفته شده، بر اساس فرکانس و جرم مودی، پاسخ آن مود از طیف طراحی استخراج شده و سپس با پاسخ مودهای دیگر ترکیب می شود تا پاسخ کلی سازه را نتیجه دهند. فرض کنید می خواهیم دو مود را در آنالیز طیفی با یکدیگر ترکیب نماییم، برآیند آنها به صورت زیر خواهد بود:

R^2 = R1^2 + 2*epsilon*R1*R2 + R2^2

در رابطه بالا حد نهایت پاسخ هنگامی خواهد بود که epsilon=1 باشد، این دقیقا مانند اینست که پاسخ دو مود را به طور کامل با یکدیگر جمع کنیم:

R^2 = R1^2 + 2*R1*R2 + R2^2

R = R1 + R2

که در عمل همان قدر مطلق جمع دو پاسخ فوق خواهد بود:

R = |R1| + |R2|

روند فوق یک عمل بسیار محافظه کارانه است. حال تصور کنید epsilon=0 باشد، که رابطه بیان شده را تبدیل به همان روش SRSS می کند:

R^2 = R1^2 + R2^2

R = SRSS(R1, R2)

 

از آنجایی که حاصلضرب عبارت R1*R2  در این روش صفر فرض می شود بنابراین به گونه ای از اندرکنش مودی در SRSS صرف نظر می کنیم. از طرف دیگر در روش CQC  از epsilon بین صفر و یک برای بدست آوردن پاسخ استفاده می شود یعنی پاسخی مابین روش SRSS و جمع مطلق مستقیم  بدست خواهیم آورد. در واقع روش CQC مقداری از اندرکنش مودی را برای مدهای نزدیک بهم لحاظ می کند و دلیل آن اینست که چنین مودهایی ممکن است با یکدیگر اندرکنش در فاز داشته باشند، بنابراین برای مودهای نزدیک بهم می بایست به صورت جبری (بدون استفاده از قدر مطلق) عمل نمود ، در حالیکه برای مودهای دور از هم می توان از روشی مانند SRSS استفاده کرد. بدلیل اینکه روش CQC دارای علامت جبری هستند نباید همیشه آنها را محافظه کارانه تر از SRSS در نظر گرفت بلکه بسته به علامت جبری روشهای CQC می توانند محافظه کارانه تر و یا غیر محافظه کارانه تر از SRSS باشد. بطور کلی بهتر است همیشه از روش CQC استفاده نماییم.

 

منبع: 
http://www.eureka.im/5132.html
@AlirezaeiChannel